Strong authentication for 2012

Not so long ago, strong authentication was equivalent to two-factor authentication. Unfortunately, things have changed quite a bit in 2011.

It is widely accepted that authenticating with only a username and password is not very secure. No matter how complex or long you make a password, it can be copied, intercepted, phished, etc. A lot of effort has been put into securing passwords. Encrypting them when stored on the server side, encrypting them while in transit (SSL/TLS), encrypting them for users that cannot remember it (KeePass, Password Safe). This does not solve the phishing problem. A user that can be tricked to enter his password in the wrong window or on the wrong site basically hands over the keys to the safe.

To protect against password theft (like phishing) one-time passwords were invented. As the name implies, these passwords can be only used once. In order to know what password to enter next, various methods exist:

• TAN list, often used by banks
• Hardware token, such as RSA or Vasco tokens
• Software token (i.e. running on a mobile phone)
• SMS message

This introduces the concept of two-factor authentication. A higher level of security can be achieved when a user is required to present two out of three categories of means to identify himself:

• Something you know (like a username or password)
• Something you have (like a physical key, a token or a mobile phone)
• Something you are (often implemented using biometrics like fingerprints, hand geometry or retina scan)

This sounds very secure, but unfortunately two-factor authentication does not protect against man-in-the-middle attacks. The classic scenario where Alice and Bob are communicating and Mallory is able to change what is being sent back and forth. Mallory and read the one-time password sent by Alice from the wire, and tell Alice that Bob is unavailable. Mallory then proceeds to authenticate against Bob using the credentials stolen from Alice.

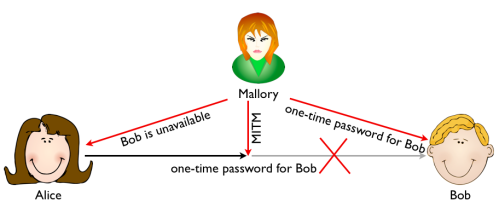
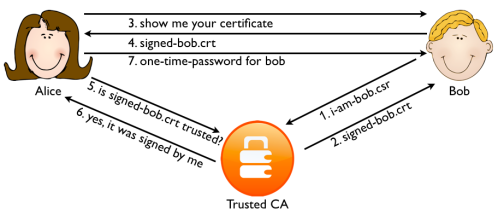
The general protection against man-in-the-middle attacks is using a Public Key Infrastructure (PKI). The most widely known PKI is probably the SSL/TLS PKI implementation used for webservers. The core idea is that servers prove their identity to a Certificate Authority (CA) that in return signs their SSL certificate. Before Alice sends her credentials to Bob, she requests his SSL certificate. Alice checks the certificate is signed by a CA she trusts. If it is not, Alice will not proceed.

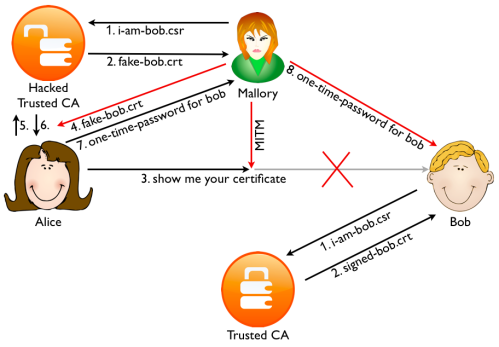
Mallory can change the certificate midway, but the idea is that she cannot present Alice with a valid certificate with Bob’s name in it that is signed by a trusted CA. This is the mechanism that is protecting the web since 1995. Coupled with two-factor authentication it was pretty strong. Until 2011 that is.

First in march 2011 an Italian reseller of the Comodo CA was hacked. Various false SSL certificates were signed for high profile sites such as Google Gmail, Yahoo Mail, and Microsoft Hotmail. Fortunately, Comodo found out and revoked the certificates before any harm could be done. Then in August a user from Iran noticed his Chrome browser gave a certificate warning when browsing to GMail. Investigation showed that a false certificate was being used by the Iranian government to intercept the traffic. The false certificate was signed by the Diginotar CA that was hacked in July 2011. These incidents show that relying on PKI server side certificates alone is not secure. The EFF SSL Observatory calculated there are around 650 organizations that function as a trusted CA in today’s browsers. Even though a server only uses a single CA for it’s certificate, an attacker can target any of the 650 CAs to get a fake one. Any certificate signed by any one of the 650 CAs will be trusted by the browser.

The only reason Google Chrome gave a warning is because both Chrome and GMail are products of Google. Google implemented an additional check for it’s own sites to see if they were indeed signed by the correct CA (SSL pinning). There have been several other proposals to fix the 650 trusted CAs issue, but they have a long way to go before they are implemented. Other solution would be to combine one-time passwords with the secure remote password protocol and TLS authentication (RFC 5054). Unfortunately browsers (like Firefox) nor web servers (like apache) support TLS-SRP at this moment.

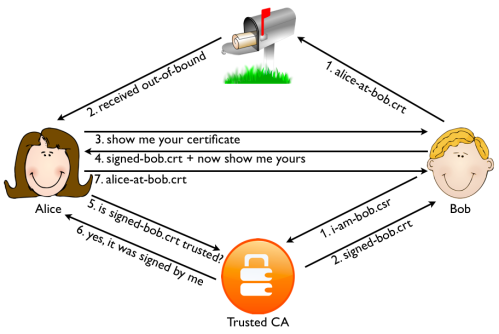
There is another solution that is available today. Instead of just using SSL server side certificates, also use SSL certificates on the client side. This means that both Alice and Bob authenticate themselves using a certificate. If Bob signs the certificates for his users himself, there is no way for Mallory to get a valid client certificate unless she hacks Bob server. But then the point of generating fake certificates is moot: whatever information Mallory is after can be read directly from the server anyway.

There is one more threat we need to protect against. Even though a certificate in itself does not possess one-time properties, because the associated private key is not transmitted it is secure against a man-in-the-middle attack. If the private key is stored in software on the client, it can be stolen if the PC is infected by a trojan or malware. This can be overcome by only storing the private key in a hardware token. This can be a smart card connected to the PC using a reader, or a PKI chip embedded in an USB stick. Of course when a client is infected with modern malware such as Zeus and SpyEye they can perform a man-in-the-browser attack. No authentication method can protect against this attack, but when the private key is stored in a hardware token, when this token is removed and the PC turned off the attacker will not be able to impersonate the users with stolen credentials. Credentials can always be stolen when a software-only solution is used.

In general strong authentication that is resistant against man-in-the-middle attacks and credential theft should:

1. use mutual authentication so that both the client and server are authenticated to the other side
2. use a hardware token which output is used in the encryption layer (like TLS)

The second property requires some explanation. There are several ways to do mutual authentication (using client certificates is just an example). A challenge response scheme that does a full challenge 1 / response 1 + challenge 2 / response 2 handshake will work, but only protects against a man-in-the-middle attack when Mallory cannot intercept both sides of the handshake. For an offline (non-USB) token TLS-SRP can be a solution when this is widely implemented.

Beyond the standard X.509 PKI solutions and tokens, I know of 2 proprietary protocols that implement mutual authentication using hardware tokens: G/On and MobiKEY.

Another solution worth mentioning is the ABN-Amro E.dentifier2 hardware token. This USB connected device contains a PKI client certificate. Crucial banking transaction are routed (using a webbrowser plugin) end-to-end from the server to the token. An LCD display shows the details of the transactions before they are signed by the device. This method seems to protect against man-in-the-browser attacks as well.